During a night of drinking at a friend’s, a question randomly came up:
Given the shape of a simple house with a cross inside of it, can you draw it with a pen without lifting it up?
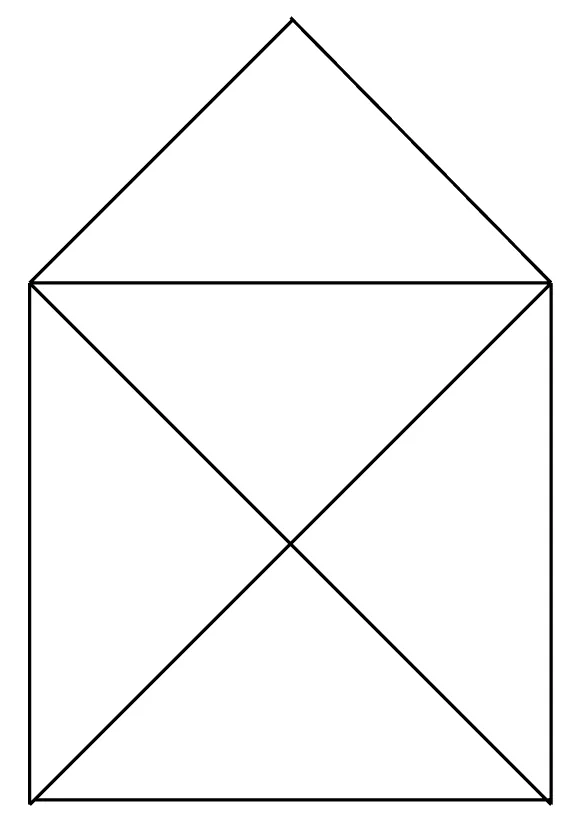
It can be figured out quite easily with a bit of time, but what’s the fun in that? Knowing a little bit of graph theory can go a long way in proving not only that a solution does indeed exist, but that all solutions have to start (and end) a particular way — from bottom of the house up.
To understand how graph theory can help, we first have to understand two things: the degree of a node in a graph, and Euler paths.
#The degree of a node
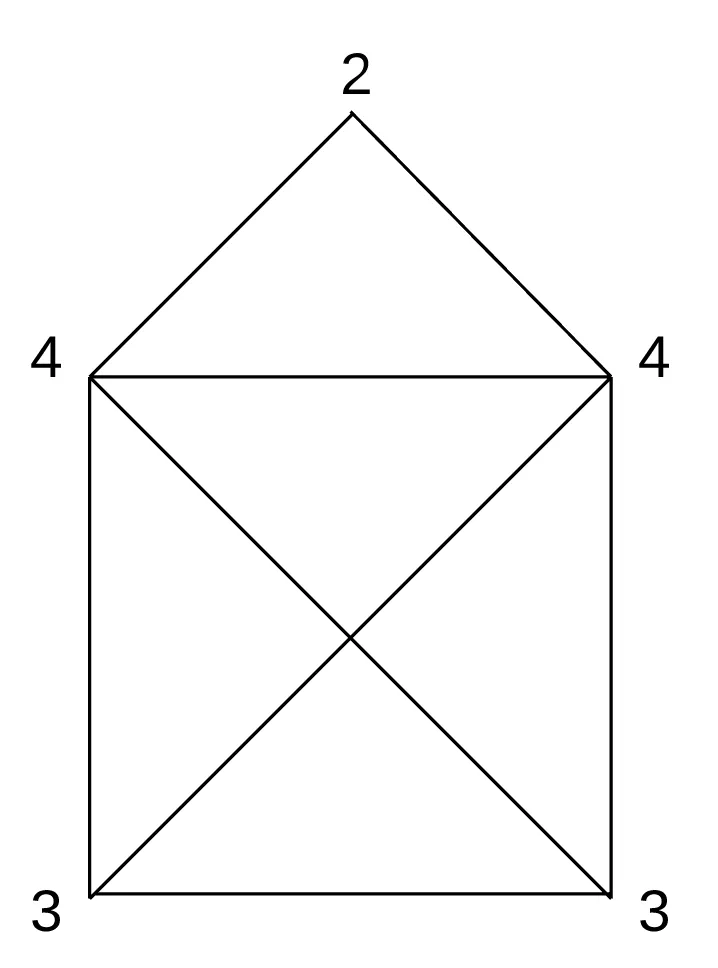
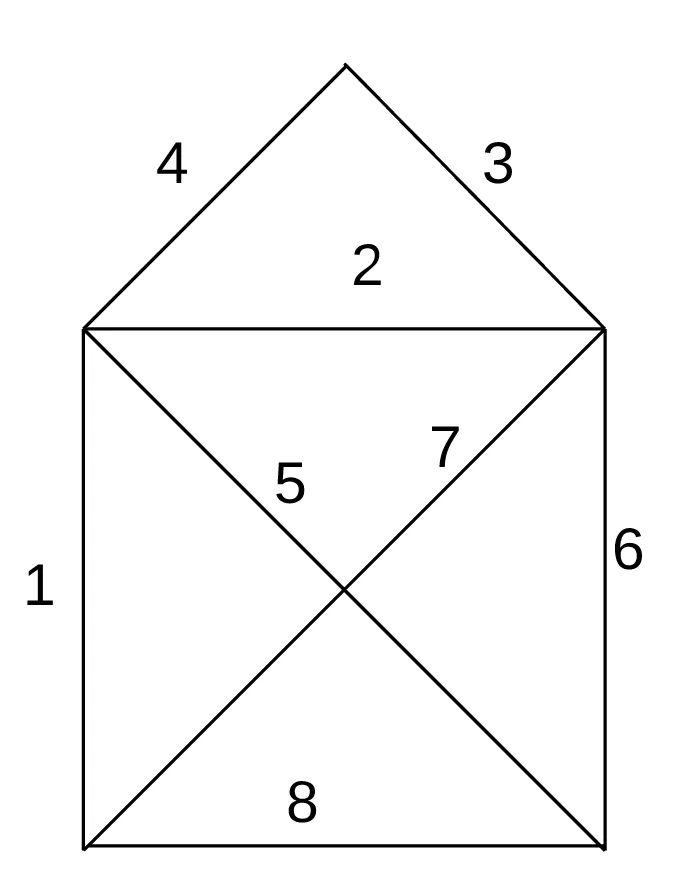
The degree of a node in a graph is how many edges are connected to it. If we annotate the house with the degree of each node, this is what it looks like:
#Euler path
An Euler path is a path taken through a graph that uses each of its edges exactly once. Notice how it maps almost perfectly to our problem?
Furthermore, we know a bit more about the existence of Euler paths in graphs. Firstly, not all graphs have Euler paths — only graphs with a particular characteristic have them. This characteristic is:
A graph that has an Euler path has at most two nodes with an odd degree.
The corollaries to this rule are:
- Aside from the above nodes with an odd degree, all other nodes must have an even degree.
- The number of nodes with an odd degree is either zero or two (since the sum of the degrees of all nodes in a graph is always even).
Why does this rule work? If we look at a few degenerate examples, it becomes clear why it makes sense intuitively.
See the following graph:
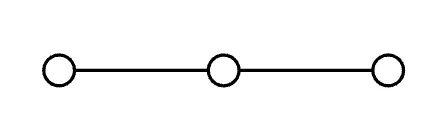
You can see that the two nodes with an odd degree will be the start and end of the path. All other nodes with an even degree represent the fact that the path will enter and exit the node equally often, and there won’t be a case where a path is “stuck”.
If there are no nodes with an odd degree, the path can start and end at any node. This is also known as an Euler circuit.
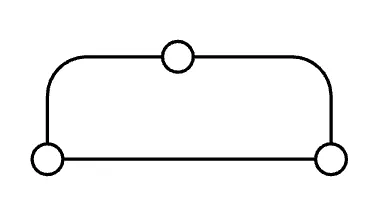
Check out this graph with one node of degree four and four nodes of degree one. It doesn’t have an Euler path.
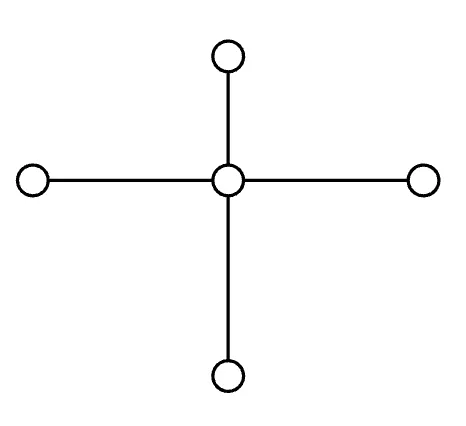
However, if we add an edge like this, it suddenly becomes possible:
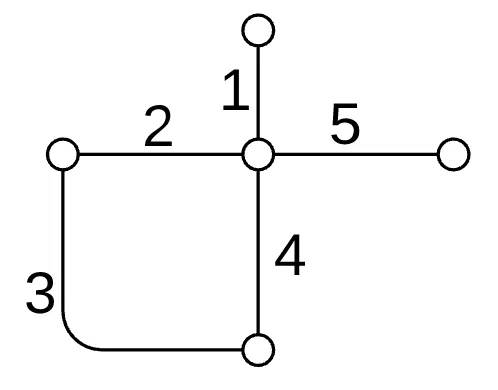
With these two concepts in mind, it becomes clear that an Euler path does exist in this house graph, as seen in the annotated graph above, shown again below:

Since the bottom two nodes are the two nodes with an odd degree, a pen trying to draw such a house must start and end at either of these two nodes, for example:
As an addendum, Euler paths should not be confused with Hamiltonian paths. A Hamiltonian path is a path taken through a graph that uses each of its nodes exactly once, instead of each edge. Finding the existence of an Hamiltonian path is much less trivial; in fact, it’s NP-complete.